2016前期 問1 b 42.86%
著作権で保護される「著作物」とは?
この問題は、著作権法で保護される「著作物」に該当するかどうかを見分ける問題です。
問題:著作権法で保護される著作物に該当しないものはどれか。
- ア.コンピュータ・プログラム
- イ.アイデア
- ウ.音楽
- エ.地図
🔍 ポイント:著作権は「表現」を守る!
著作権で守られるのは、「創造的な表現」や「見せ方」です。 その中身の「アイデア」や「事実そのもの」は対象外です。
✅ 保護されるものの例
| 選択肢 | 保護理由 | 具体例 |
|---|---|---|
| ア.コンピュータ・プログラム | ソースコードや設計は「表現」 | 書かれたコード、UI設計など |
| ウ.音楽 | メロディや歌詞は創作された「表現」 | 楽譜、音源 |
| エ.地図 | 表現の仕方に工夫がある | 図形の配置、色、情報の選び方 |
🚫 保護されないものの例
| 選択肢 | 保護されない理由 | 補足 |
|---|---|---|
| イ.アイデア | 表現ではなく「考えそのもの」だから | 誰でも自由に使えるべき概念や発想 |
🧠 補足:アイデアと表現の違い
- 「空飛ぶ靴で冒険する物語」は… → アイデア(×保護対象外)
- 「その物語を小説や漫画にしたもの」は… → 表現(○著作権で保護)
🎯 結論
- 正解は → イ.アイデア
✨まとめ(超重要)
- 著作権で守られるのは 思いつき(アイデア)ではなく、形にしたもの(表現)!
- 「表現の工夫があるか」が判断のカギ!
🧾この問題の整理:
- ア → プログラムのコードは表現 → 保護対象
- イ → アイデアそのもの → 保護されない!(正解)
- ウ → 音楽(作曲)は創造的な表現 → 保護対象
- エ → 地図も工夫された表現 → 保護対象
🎓 アイデアは自由。表現は守られる!
—
2016 前期 問1d
写真のブログ掲載に必要な許可とは?
問題文:
写真に写っている人物(Aさん)の友人(Bさん)が、その写真(図1)を自分のブログに載せたいと考えている。
著作権法上、図1をブログに載せるには、Aさんからどんな許可や同意を得る必要があるのか?
選択肢:
- ア.Aさんの展示権
- イ.Aさんの個人情報公開について
- ウ.Aさんの上映権
- エ.Aさんの複製権と公衆送信権 ← ✅正解!
—
📌 そもそも何が問題になっているの?
写真には「撮った人の権利(著作権)」と「写っている人の権利(肖像権など)」があります。 この問題では、「撮った人=Aさん」、「写っている人=Bさん」、その写真を使いたい人もBさんです。
つまり、Bさんが勝手にAさんの写真をネットに載せようとしている状態。
→ この場合、著作権を持つAさんの許可が必要です。
—
✅ 著作権の中で必要な許可は?
| 権利名 | 内容 | 今回関係するか |
| ——– | —— | —————- |
| 複製権 | コピーを作る権利 | ✅ 写真をブログにアップする=コピーを作る |
| 公衆送信権 | インターネットなどで配信する権利 | ✅ ブログに載せる=ネット配信 |
→ よって エ.複製権と公衆送信権 の許可が必要!
—
❌ 間違いやすい選択肢たち
- ア.展示権:展覧会などで「現物を展示」する権利 → ブログは関係ない
- イ.個人情報公開:写真の肖像権やプライバシーの話だけど、著作権とは別問題
- ウ.上映権:動画や映画などを「スクリーンで映す」場合に必要 → 写真は関係ない
—
🧠 補足:写真の著作権は誰のもの?
- 基本的に「撮影した人」にあります(この場合はAさん)
- 写っているだけの人(Bさん)には著作権はないけれど、「肖像権」はある
—
🎯 結論:
- BさんがAさんの写真(図1)をブログに載せるには、
- Aさんの著作権(複製権+公衆送信権)に対する許可が必要!
→ 正解は:**エ.Aさんの複製権と公衆送信権**
—
📷 勝手に写真をアップしてはダメ!
- ブログに写真を載せる=コピーして公開する
- それには「著作権者の許可」が絶対必要!
- 撮った人がAさんなら、使いたい人(Bさん)はAさんに許可をとろう!
2016前期 問20b 17.86%
陰関数で表される2次曲線とは?
問題文:
陰関数の形で表される平面曲線は、関数 f(x, y) = 0 を満たす点の集まりとして定義できる。
その f(x, y) が 2次多項式(2次式)のとき、その曲線は何と呼ばれるか?
選択肢:
- ア.コッホ曲線
- イ.ベジエ曲線
- ウ.パラメトリック曲線
- エ.円錐曲線(正解 ✅)
🧠 陰関数ってなに?
陰関数とは、xとyの関係が明示的にy=〜と解かれていない形の式:
- 例:
`f(x, y) = x² + y² − 1 = 0` ← これが陰関数
この式が表すのは、「x² + y² = 1」すなわち単位円!
→ このように「式が0になる点の集まり」で曲線を定義するのが陰関数表現。
✏️ 2次の陰関数で表される曲線のことを?
2次式(=2次多項式)で表される陰関数:
\[ f(x, y) = Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 \]
この形で表される曲線は、数学的に 円錐曲線(conic section)と呼ばれます。
✅ 円錐曲線とは
円錐曲線には次のような形がすべて含まれます:
- 円(x² + y² = r²)
- 楕円(x²/a² + y²/b² = 1)
- 放物線(y = ax²)
- 双曲線(x² − y² = 1)
→ これらはすべて「2次の陰関数」で表せる!
—
❌ 他の選択肢との違い
- ア.コッホ曲線:フラクタル図形(無限のギザギザ)、全く別物
- イ.ベジエ曲線:制御点とパラメータで定義される曲線、形は自由だが陰関数ではない
- ウ.パラメトリック曲線:x(t), y(t) のようにパラメータで表される曲線 → 陰関数ではない
—
🎯 結論
- f(x, y) = 0 が2次式のとき、その曲線は「円錐曲線」または「2次曲線」と呼ばれる!
→ 正解は:**エ.円錐曲線**
—
🌀 陰関数で表せる代表的な曲線たち
- 円 → x² + y² = r²
- 放物線 → y = ax² ⇔ ax² − y = 0
- 楕円 → x²/a² + y²/b² = 1
- 双曲線 → x²/a² − y²/b² = 1
これらすべてが「2次の陰関数」=円錐曲線!
2016前期 問23b 46.43%
🧊 光の反射やガラスのような見た目を作るには?
(2)図2に示すような周囲の物体が映り込んだ画像や、図1に示すような画像を生成するのに適した手法は [a] である。
【解答群】
ア.ラジオシティ法 イ.スムーズシェーディング ウ.Zバッファ法 エ.レイトレーシング法
正解:エ.レイトレーシング法
🌈 わかりやすい解説
図2を見てみよう!
- 真ん中のドーナツみたいな形が、ガラスみたいに透明だね。 - 周りの床や他の物体が映り込んでいるのが分かるかな? - これは、光が反射したり、物を通り抜けたりする様子を、とてもリアルに再現してるんだ!
こういう「本物そっくりの画像」を作るときに活躍するのが……
👉 レイトレーシング法(Ray Tracing)!
💡 レイトレーシング法ってなに?
レイトレーシング法は、こう考えるんだ:
1. 目(カメラ)から光線(レイ)を出す 2. その光がどこにぶつかるかを調べる 3. ぶつかった場所からまた反射・屈折をシミュレーション! 4. 最終的にどんな色になるかを計算!
☀️ 本当の光の動きをまねするから、とってもリアルな画像になる!
🚫 他の選択肢と何が違うの?
- ア.ラジオシティ法:間接光(部屋の中の光の跳ね返り)を計算する方法。反射や透明は苦手。
- イ.スムーズシェーディング:物の表面をなめらかに見せるだけ。映り込みはできない。
- ウ.Zバッファ法:どれが前にあるかを判断するだけ。リアルな光の計算はしない。
- エ.レイトレーシング法:反射・透過・影・屈折ぜんぶできる!
🎯 まとめ
* ガラスや鏡のような表現をしたいときは、 → レイトレーシング法が一番リアルでぴったり!✨
🖼️ キラキラした映り込み画像を作りたいときは?
🎓 問題の構造
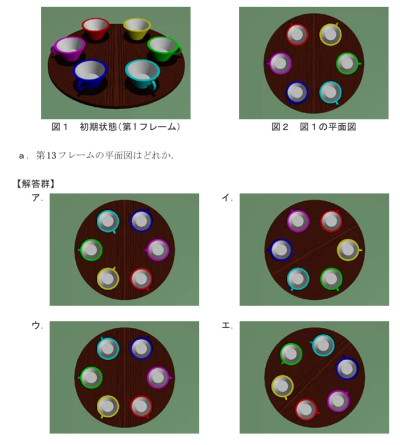
■ 図1(初期状態)について
テーブルの上に、カラフルな取っ手付きカップが 8 個あります。
各カップは、縁の色が異なっており、取っ手の向きにも規則性があるように見えます。
↓それを真上から見たのが…
■ 図2(第1フレームの平面図)
時計回りに:
- 赤 → 桃 → 紫 → 緑 → 黄 → 水 → 青 → 白
色の順番が固定されています(この順番が「座席」番号になります)
🔍 ルールを探る
ここでのカギは:
- カップの 回転(取っ手の位置)
- または 入れ替え(色の並びの変化)
Step 1:図1 → 図2 の変化を確認
図1(初期)を斜めから見たとき、 取っ手はすべて自分側(手前)に来るように配置されています。
図2(真上)になると、取っ手が「右・左・上・下」などに変化して見えています。
これはカップの回転の結果です!
→ つまり、「取っ手の向き」が変化していく=カップが回転している
🧠 仮説:カップは1フレームごとに 90度回転?
実際に第1フレーム(図2)から見て:
- 赤:取っ手が上
- 桃:取っ手が右
- 紫:取っ手が下
- 緑:取っ手が左
- …
とすると、各カップの取っ手が時計回りに 1/4 回転していくと仮定できます。
✅ 第13フレームの法則
1フレームで90度(=1/4回転)するなら、
→ 13フレームでは 13 × 90 = 1170度 回転
→ 1170 ÷ 360 = 3回転 + 90度
→ 結局、初期状態から 「90度だけ回転」 した状態になる!
🎯 答えの見つけ方
第1フレーム(図2)と比べて:
→ 取っ手がすべて 1つ分だけ時計回りにズレた図を探す!
図2と各選択肢を比較
- 色の順番は同じ(赤 → 桃 → 紫 → 緑 → …)
- 取っ手の位置だけが変化
- 全体が1個分時計回りにずれているものを探す!
🏁 結論
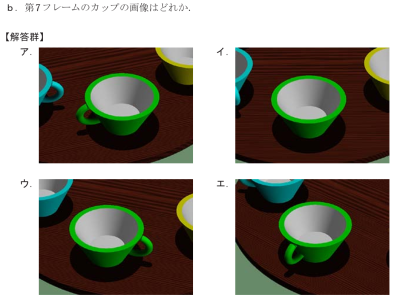
🧩 第7フレームのカップ画像を選ぶ問題
■ 前提
前問(a)では「1フレーム=カップが時計回りに90度(=1/4回転)」というルールを導きました。
つまり、第7フレームなら、初期状態から「7×90°=630°回転」していることになります。
630 ÷ 360 = 1回転 + 270度 → 結果的に “270度(=右向き)” 回転した状態になる!
🔍 ステップで整理!
▶ 初期状態のカップ(図1)を思い出す: カップの 取っ手はすべて手前(画面下方向) に向いていました。
そこから、1フレームごとに90°ずつ時計回りに回るので、回転角ごとの取っ手の位置は次のようになります:
| フレーム数 | 回転角度 | 取っ手の位置 |
|---|---|---|
| 0(初期) | 0° | 下(手前) |
| 1 | 90° | 左 |
| 2 | 180° | 上(奥) |
| 3 | 270° | 右 |
| 4 | 0° | 下 |
| 5 | 90° | 左 |
| 6 | 180° | 上 |
| 7 | 270° | 右(←これ!) |
🎯 結論:第7フレームでは「取っ手が右側」になる!
選択肢を見てみましょう:
- ア:取っ手が左(❌)
- イ:取っ手なし(背面で見えない=上 or 下)(❌)
- ウ:取っ手が右!(✅ 正解!)
- エ:取っ手が手前=下(❌)
🏁 最終結論
🧩 問題 c:図3の状態になるのは第何フレームか
■ 問題概要
図3のように、6つのカップが特定の向きになっている状態が、最初に現れるのは第何フレームか?
■ 観察ポイント
各カップの「取っ手の位置」に注目! 回転だけでなく、色の並び順(座席順)は固定と考えてよい。
■ 初期状態のルール(復習)
各カップは 1フレームごとに時計回りに90度 回転。
つまり:
| フレーム数 | 回転角度 | 取っ手の位置 |
|---|---|---|
| 0(初期) | 0° | 下(手前) |
| 1 | 90° | 左 |
| 2 | 180° | 上(奥) |
| 3 | 270° | 右 |
| 4 | 0° | 下 |
| 5 | 90° | 左 |
| 6 | 180° | 上 |
| 7 | 270° | 右 |
| 8 | 0° | 下 |
| … | … | … |
→ 4フレームごとに、取っ手は元に戻る周期がある!
🔍 図3を詳しく観察
それぞれのカップの色と取っ手の向きを確認:
- 赤:左
- 黄:左
- 緑:上
- 水:右
- 青:右
- 桃:下
これを、初期状態(図1)から何フレーム進めばこの取っ手の位置になるかを調べる。
▶ 色ごとの回転を調査
以下に、初期状態(図1)での各カップの取っ手の位置を「下」として、 そこから回転して図3と同じ方向になる最小のフレーム数を見てみる:
| 色 | 図3での取っ手位置 | 回転角 | 必要フレーム数 |
|---|---|---|---|
| 赤 | 左 | 90° | 1フレーム |
| 黄 | 左 | 90° | 1フレーム |
| 緑 | 上 | 180° | 2フレーム |
| 水 | 右 | 270° | 3フレーム |
| 青 | 右 | 270° | 3フレーム |
| 桃 | 下 | 0° | 0フレーム |
→ 共通のフレーム数がない!
でも、周期性があるので「全員がその位置になるフレーム」を見つければOK!
▶ 取っ手の位置の周期性
取っ手の回転は 4フレームごとに 1周(360°)する。
つまり、例えば赤の「左」向きは
- フレーム1
- フレーム5
- フレーム9
- フレーム13
- フレーム17 …
と 4n+1 フレームで現れる。
同様に、各向きのタイミングを次にまとめる:
| 向き | フレームの形(nは0以上の整数) |
|---|---|
| 下 | 4n |
| 左 | 4n+1 |
| 上 | 4n+2 |
| 右 | 4n+3 |
図3の6つのカップの向きが同時に現れる最小のフレームを探すと…
すべて満たすのは → フレーム19
🏁 結論
✅ 正解:エ. 第19フレーム
理由:
- 赤・黄:左(4n+1) → 19でOK
- 緑:上(4n+2) → 18+1=19でOK
- 水・青:右(4n+3) → 16+3=19でOK
- 桃:下(4n) → 16+3=19でOK(←周回周期)
→ 全色の条件を満たす 最初のフレームが「第19フレーム」
問24 d 53.57%
🧮 問題 d:台が4回転するのに何秒かかるか
■ 問題文
台が毎秒12フレームで回転する場合、その台が4回転するには何秒必要となるか。
■ 考え方
この問題では、以下の情報が与えられています:
- 1回転に必要なフレーム数:4フレーム
(前の問題から、カップの回転周期は4フレーム=1周と判明)
- 毎秒12フレーム進む(=12フレームで1秒)
→ つまり、1回転=4フレームにかかる時間は…
- 1秒で12フレーム → 1フレーム=1/12秒
- 4フレーム=(1/12)×4=1/3秒
▶ 4回転分を計算
- 1回転 = 1/3秒
- 4回転 = 4 × (1/3) = 4/3秒 × 3 = 4秒
🏁 結論
✅ 正解:ア.4秒
■ 補足
他の選択肢は:
- イ.6秒 → 6×12=72フレーム=18回転(回りすぎ)
- ウ.8秒 → 8×12=96フレーム=24回転(回りすぎ)
- エ.12秒 → 12×12=144フレーム=36回転(大回り)
→ どれも過剰な時間。
4秒がぴったり!
問27 a 46.43%
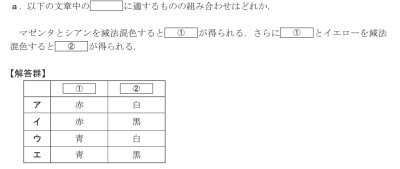
🎨 減法混色の色の組み合わせ問題
■ 問題文(要約)
マゼンタとシアンを減法混色すると ①が得られる。 さらに、①とイエローを減法混色すると ②が得られる。
🔍 減法混色の基本
減法混色とは、光ではなく「インク」や「絵の具」などの色材を混ぜるときのルールです。
- 減法三原色は:
- シアン(C)・マゼンタ(M)・イエロー(Y)
- 減法混色の基本的な組み合わせ:
| 組み合わせ | 結果の色 |
|---|---|
| マゼンタ + シアン | 青(Blue) |
| マゼンタ + イエロー | 赤(Red) |
| シアン + イエロー | 緑(Green) |
| C + M + Y 全部混ぜる | 黒(Black) |
▶ ステップ1:①を求める
マゼンタとシアンを混ぜる → 青
→ よって、①は 青
▶ ステップ2:②を求める
①の青(=マゼンタ+シアン)とイエローを混ぜる
つまり、シアン+マゼンタ+イエロー(CMY全部)を混ぜる
→ 結果は 黒
→ よって、②は 黒
🏁 正解
- ①=青、②=黒 → 選択肢「エ」
✅ 正解:エ
🧠 補足:混乱ポイント
- 「光の三原色(RGB)」と混同しやすい!
- 光(加法混色)なら、R+G+B=白 になるが、
インク(減法混色)では、CMY=黒になる。
📘 まとめ
🎨 問題の概要
グレースケール画像(図4)に対し、RGBチャンネルごとに異なるトーンカーブを適用することで、カラー擬似画像(図5)を生成しています。 このとき使われたトーンカーブ(ア〜エ)のうち、図5を最もよく再現するものを選ぶ問題です。
🔍 図5の色の観察
図5の色分布の特徴は次の通り:
- 暗い部分:緑〜青系(寒色)
- 中間の明るさ:青〜マゼンタ系
- 明るい部分:赤〜ピンク系(暖色)
⇒ 明るさによって色が変化している
📈 トーンカーブの読み取り
それぞれの選択肢について、R/G/Bのトーンカーブの傾向を確認します。
ア
- R:直線増加
- G:直線減少
- B:直線増加
- → 明るさが増すほど赤と青が強くなり、緑が減る → マゼンタ系に近づく
イ
- R:減少
- G:増加
- B:直線増加
- → 緑と青が強く、赤が抑えられる → 寒色寄り(全体が暗く見える)
ウ
- R:逆V字(中間最大)
- G:常にゼロ
- B:V字(中間最小)
- → 極端な色の変化。緑がゼロでバランス悪い → 不自然な画像
エ
- R:V字(暗所と明所で赤)
- G:逆V字(中間で緑強め)
- B:直線増加
- → 色の揺れが激しい → 図5のようなスムーズな変化とは異なる
🎯 判断ポイント
図5のように、
- 暗所が寒色(青・緑)
- 明所が暖色(赤・マゼンタ)
を表現するには:
→ ア のトーンカーブが最も適している
✅ 正解
正解:ア.
- 明るさに応じて、RGBのバランスが変化し、自然な疑似カラーが得られる